Basic Op Amp Model

Basic Op Amp Model

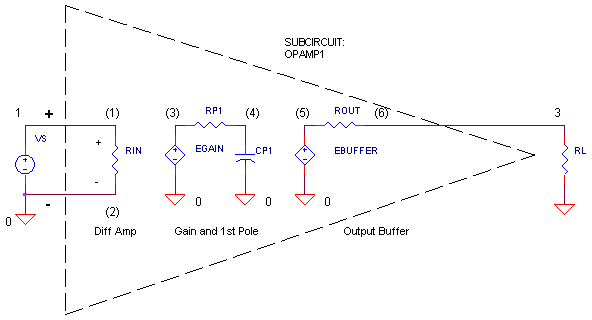
CIRCUIT

OPMODEL1.CIR Download the SPICE file

One of the challenges of simulating opamp circuits is modeling the op amp itself. How is that accomplished? There's a couple of ways. You can create a circuit of many transistors, resistors and caps that closely replicate the internals of an op amp. Or, you can create a simpler model that reproduces the basic behavior of the op amp. The benefit of the simpler model is one that uses less components and typically simulates faster. As you begin to look at more complex or subtle behaviors, you can create a more complex op amp model.

To simulate more complex behaviors, check out the Intermediate Op Amp Model. For a description of all available op amp models, see Op Amp Models.

OP AMP MODEL

What are the three basic stages of an op amp? The circuit above shows 1) a differential amplifier, 2) a voltage gain stage with single-pole frequency roll-off and 3) an output buffer. (As a convenience, we'll define this model as a subcircuit. See Why Use Subcircuits?)

The subcircuit models the following behaviors:

Input impedance RIN
Differential Gain EGAIN
Single Pole Frequency RP1, CP1
Output Impedance ROUT

If you're designing a precision amplifier, you can see how gain and input / output resistance effect accuracy. If your designing a high-speed amplifier, you can determine your circuit's bandwidth. You can also see how stray and load capacitances may cause your amplifier to ring or oscillate.

OPEN-LOOP FREQUENCY RESPONSE

The open-loop response gives you some powerful insight into the op amp’s performance. Open-loop means NO feedback; the response of the “naked” op amp. Two important features are

1. DC Gain – the gain at DC. ( The more you have, the more accurate your amplifier. )

2. First-Pole Frequency, fp1 – the frequency where the open-loop begins to fall. A direct result of fp1 and the DC Gain is the Unity-Gain Frequency, fu – the frequency where the open-loop gain falls to 1 V/V. The greater the fu, the faster your op amp can respond.

CIRCUIT INSIGHT The op amp is driven by AC source VS. There are no feedback resistors here – its running open-loop. Try out the model by running a simulation and plotting the AC magnitude VM(3). Can you see the DC gain = 100k V/V and the first-pole at fp1 = 100 Hz? What is the unity gain frequency? Try changing the Y-Axis to a log scale to get a better view at high frequencies. If your plotting in dB, the unity-gain level is 0 dB.

You might ask, what if I don’t need a gain of 100k V/V? Op amps are actually intended for lower gains set by feedback resistors connected around the device (Closed-Loop Gain). The higher the internal gain (like 100k V/V and above) the more accurate your lower Closed-Loop Gain will be (set by the feedback resistors only.)

UNITY-GAIN FREQUENCY

As stated before, the greater the unity-gain frequency, the faster your op amp can respond. What determines the this frequency? It’s set by the DC Gain and fp1.

where the pole frequency is formed by a simple RC filer

HANDS-ON DESIGN Suppose you need to model an op amp with the same DC gain but a higher unity-gain frequency fu. Simply solve for a new fp1 in the 1st equation. Then, calculate the new CP1 from the 2nd equation to achieve that desired fp1. For example,

Choose a new fu, such as 50 MHz.
Then, calculate fp1 = fu / DCGAIN = 50 MHz / 100 k = 500 Hz
CP1 = 1/( 2 * π * 1k * 500 Hz) = 0.318 uF.

Try out your new op amp model. Did the magnitude VM(3) hit the unity-gain where you expected?

PHASE SHIFT

CIRCUIT INSIGHT So far we’ve looked at the gain / attenuation of the input signal by the op amp. At some point, you may need to know the phase shift (time shift) as well. To check out the phase shift, add another plot to the window, then, add trace VP(3) where the P tells SPICE to display the Phase. A maximum of -90 degrees of phase shift should occur beyond the first pole fp1.

What’s the big deal about phase anyway? Turns out, the phase shift (and gain) of the signal in a feedback circuit reveals how well a circuit performs. Too much negative phase can cause an amplifier circuit to overshoot, ring or even oscillate. Knowing the phase shift will help you fix the problem. On the other hand, if you’re designing an oscillator, you’ll need to know how to add the right amount of phase at the right frequency. More on these topics in Op Amp Feedback Analysis.

OP AMP CIRCUITS

This op amp model is used for the innards of many op amp circuits in this site: Inverting Amplifier, Non-Inverting Amplifier, etc. Go ahead and turbo-charge some of the op amps by upping the Unity-Gain Frequency of the model and checking out its effect on the closed-loop bandwidth (with feedback components) of the amplifier.

SIMULATION NOTE

The op amp model is created from several simple SPICE devices. The differential input and DCGAIN stage are implemented by a Voltage-Controlled Voltage Source (VCVS) named EGAIN. The device

EGAIN 3 0 1 2 100K

follows the syntax

E{name} {+output} {-output} {+control} {-control} {gain}

which creates a voltage source having positive and negative output terminals at nodes 3 and 0. The source is controlled by the voltage at positive and negative sense leads 1 and 2. This voltage is then multiplied by the gain 100k and applied at the output terminals. The output buffer EBUFFER is simply another VCVS.

SPICE makes three other controlled sources available: a Current-Controlled Voltage Source (CCVS), a Voltage-Controlled Current Source (VCCS) and Current-Controlled Current Source (CCCS). Check them out at the SPICE Command Summary.

RELATED TOPICS

To simulate more complex behaviors, check out the Intermediate Op Amp Model.
See a description of all available op amps at Op Amp Models.
For a quick review of subcircuits, check out Why Use Subcircuits?
Get a crash course on SPICE simulation at SPICE Basics.
To see how open-loop gain and bandwidth influence closed-loop bandwidth, see Op Amp Bandwidth.
This op amp model can be used many of the op amp circuits available from the Circuit Collection page.

SPICE FILE

Download the file or copy this netlist into a text file with the *.cir extention.

OPMODEL1.CIR - OPAMP MODEL SINGLE-POLE
*
VS 1 0 AC 1
XOP 1 0 3 OPAMP1
RL 3 0 1K
*
* OPAMP MACRO MODEL, SINGLE-POLE
* connections:      non-inverting input
*                   |   inverting input
*                   |   |   output
*                   |   |   |
.SUBCKT OPAMP1      1   2   6
* INPUT IMPEDANCE
RIN 1 2 10MEG
* DC GAIN=100K AND POLE1=100HZ
* UNITY GAIN = DCGAIN X POLE1 = 10MHZ
EGAIN 3 0 1 2 100K
RP1 3 4 1K
CP1 4 0 1.5915UF
* OUTPUT BUFFER AND RESISTANCE
EBUFFER 5 0 4 0 1
ROUT 5 6 10
.ENDS
*
* ANALYSIS
.AC  DEC  5 1 100MEG
* VIEW RESULTS
.PLOT AC  VM(3)
.PROBE
.END

The operational amplifier

0. Introduction

An operational amplifier, op-amp, is nothing more than a DC-coupled, high-gain differential amplifier. The symbol for an op-amp is

It shows two inputs, marked “+” and “-“ and an output. The output voltage is related to the input voltages by V_out = A(V₊ - V_-). The open loop gain, A, of the amplifier is ranges from 10⁵ to 10⁷ at very low frequency, but drops rapidly with increasing frequency. Furthermore, A is strongly dependent on temperature, supply voltage etc. For this reason the op-amp becomes only truly useful when the overall circuit properties are primarily determined by a feedback loop instead of the open loop gain. Thus, in the following exercises, with the use of a voltage divider, part of the output voltage is fed back to the “‑“ input.

• An amplifier will not work without a power supply. And a more complete diagram looks like the figure below, which also indicates the standard pin configuration.

Figure 1. Op-amp with pin configuration

• The pin connections on op-amps are to a very high degree standardized. IC pins are numbered counter clockwise (looking from the top) and for 8-pin op-amps you will always find

Pin	Function
2	Inverting input
3	Non-inverting input
4	V- supply
6	Output
7	V+ supply

The other pins are used for offset adjustment or frequency compensation, and are of less importance.

• Note that a positive and a negative supply voltage are shown, but no ground or zero potential. This doesn’t mean that your ground can just float. You have to provide return paths for the input and output currents ! The absence of a ground pin only indicates that the op-amp has no intrinsic, build in reference point.

• Most of the time the connections for the power are not indicated in the circuit diagrams, and in this lab manual you will not find them either. Everywhere it is assumed that the op-amp gets connected to the +/- 12V power on the prototyping board.

• More modern op-amps are difficult to destroy, but one thing that usually does them in is interchanging the connections to the power supply. Make sure that you clearly understand the pin configuration before you wire the circuit and switch on the power.

There are a number of op-amps available in the lab. For these initial exercises you should use an OP27.

1. Inverting and non-inverting amplifiers

There are two basic types of amplifiers, the non-inverting amplifier shown in figure 2, and the inverting amplifier discussed later in this section.

Figure 2. The basic non-inverting op-amp circuit, two possible representations of the same circuit.

The low-frequency gain of the non-inverting amplifier is set by the resistors R1 and R2, A = 1 + R1/R2. For a gain of 1 these resistors can be omitted and the output is directly connected to the inverting input (Fig. 3). The input impedance of this amplifier is very high, but you should keep in mind that a path has to be provided for the input current into the non-inverting input. Here, this is take care of by R3. Using a potentiometer and series resistor to provide a dc input voltage, measure the gain of this circuit for a number of values for R1 and R2 in the 1 -- 100 kW range. Also check that the unity gain buffer, fig. 3, does provide a gain of exactly 1.

Figure 3. The unity gain buffer.

The inverting amplifier (fig. 4) has a gain A = -R2/R1. Note that |A| can be smaller than 1. One complication with the inverting amplifier is that the input impedance is rather low (R1), and that the gain of the circuit is influenced by the output impedance of the source. To check that this circuit works, repeat the measurements that you did for the non-inverting amplifier, preferably using the same resistors. Note the change in the sign of A, and that |A_inv| = |A_non-inv| - 1.

Figure 4. The inverting amplifier.

2. Adding and subtracting

Operational amplifiers got their name because one can perform a number of mathematical operations with them. The simplest operations are addition and subtraction. Figure 5 shows a typical (inverting) adder. The output voltage is given by Vout = -[(Rf/R1) V1 + (Rf/R2) V2). By making R1 = R2 signals are added with equal weight, but this does not necessarily have to be the case. Test this circuit for a range of positive and negative input voltages. Do this for R_f = R1 = R2 = 10 kW and for R_f = 50 kW, R1 = 20 kW, R2 = 10 kW.

Figure 5. The (inverting) adder. (including a resistance-potentiometer networks to set V1 and a function generator to control V2.)

Subtraction is done with a circuit that is usually called a differential amplifier (fig. 6). When R1 = R3 and R2 = R4, Vout = (R2/R1) ´ (V2 – V1), i.e., the output voltage is proportional to the difference between V2 and V1 and the gain A = R2/R1. Take R1 = R3 = 10 kW, and R2 = R4 = 100 kW, and again test the circuit for a number of input voltages.

Figure 6.

The differential amplifier

3. Integration and differentiation

Two other fairly easy operations that can be performed using op-amps are integration and differentiation. If the op-amp were ideal, an integrator (Fig. 7) would require just one resistor, R, and one capacitor, C, and the relation between the output and input voltages would be given by

However, the input offset voltage, which for a non-ideal op-amp is not zero, also gets integrated. As a result the output voltage starts to drift. To fix this R_f is added to the circuit. This makes the gain for very low frequency signals finite again, but of course this means that signals with frequency components below a certain value (f <>2pR_f C) are not properly integrated anymore.

The integrator is most conveniently tested using a function generator and oscilloscope. First qualitatively check that square waves are integrated to triangles, triangles to parabolas etc. Then measure the ratio Vout/Vin as a function of frequency (with a sine-wave input signal). Compare with the expected behavior.

Figure 7. The integrator

Initial values

R = 10 kW

C = 10 nF

R_f = 1 MW

By switching R and C, you get a differentiator (Fig. 8). This circuit is intrinsically unstable and will start to oscillate a high frequency. To avoid this, you can reduce the high frequency gain of the circuit by adding C_f. (Often, stray capacitance is enough to stabilize the circuit, but it tends to be noisy.) The price you pay is that the circuit doesn’t function as a differentiator for frequencies, f > 1/2pR C_f. Again, the circuit is most conveniently tested with a function generator and an oscilloscope. A triangle wave input should be differentiated to a square wave, a square wave to alternating positive and negative going pulses.

Operational Amplifiers

Op amps are versatile ICs containing a hundred or so transistors that can perform a vareity of mathematical functions. For this reason, they are the building blocks of many signal processing circuits. They have two inputs, an inverting (-) and noninverting (+). A positive voltage source and negative voltage source or ground are connected directly to the op amp, although these are rarely shown on circuit diagrams. There is a single output, which is almost always connected to the inverting input with a negative feedback loop.

Op Amps have almost infinite gain, high input impedance, and low output impedance. Because of this, they serve many useful purposes in analog circuits. Some of these properties are discussed in the context of the following examples.

All of the example circuits can be analyzed by observing the following simple rules.

1. The output does whatever is necessary to make the voltage difference across the inputs equal to zero.
2. The inputs draw no current.
3. The output voltage does not depend on the output current.

Even though there is a lot going on inside the op amp, these rules describe its "black box" integrated circuit behavior. Ideal op amps are modeled with infinite gain and infinite impedance - real op amps only approximate these model properties. Likewise, while our model assumes infinite voltage gain, the limiting output voltage magnitude is about 1.4V lower than the magnitude of the supply voltage (this is due to diode drops in the op amp). Some of these effects should be observable if we apply a square wave input. At the rising and falling transitions of the square wave the voltage changes infinitely fast and while they're fast, op amps can't change instantaneously - there should be a slightly non-vertical slope produced in the output. This can be measured by the slew rate (with is the change in voltage over the change in time).

Inverting Amplifier - This configuration copies an inverted and scaled version of the input signal to its output. In doing so, the circuit isolates the circuit that produces the input reference from the circuit that uses the output by virtue of our op amp's impedance relationships.

Non-Inverting Amplifier - We can accomplish amplification without inversion if we re-configure the circuit slightly.

By setting R₂ to zero (short circuit) and R₁ to infinity (open circuit to ground), we get a non-inverting, unity gain amplifier - the unity-gain follower. This is an important use of operational amplifiers. The high input impedance of the amp draws virtually no current and so acts as an impedance buffer. One could, for instance, use a voltage divider to step the voltage used to drive a resistive load down without worrying about impedance loading the divider. The op amp lets you track the input voltage without drawing significant current.

Integrating and Differentiating Amplifiers - By using a capacitance, the op amp can compute the integral and differential of the input voltage. In the first example, we see that the output voltage is the integral of the input voltage.

And by switching the capacitor and the resistor, the output voltage is the derivative of the input voltage with respect to time.

Adder - This circuit produces and output equal to the negative weighted sum of the respective inputs. One can imagine that with the right input resistances, we could construct a form of D/A converter with in which input "bits" are amplified by an amount proportional to their position in a binary word.

Comparator - This setup is used to determine which input signal is greater. When the inputs are equal, there is no output. When the inverting input is greater, the op amp becomes saturated and output voltage is equal to the positive voltage supply. When the inverting input is greater, the output voltage is equal to the negative voltage supply. There are TTL comparators available that would be recommended for this purpose, but the mighty op amp can do it in a pinch.

LM 741

	The LM 741 is a single OP-AMP in an 8-pin chip. It is the most widely-used op-amp in the world. It can operate from a single 9v supply or up to +18v/-18v (741C). As the frequency increases, the maximum gain decreases. Unity gain occurs at 1.5MHz.
	See our 3 page article on OP-AMPs in the subscription section: Basic Electronics Course pages 72, 73 and 74. It shows an animated OP-AMP with varying voltage on the inputs and the voltage on the output.

Operational Amplifier (Op-Amp) Basics

The op-amp is basically a differential amplifier having a large voltage gain, very high input impedance and low output impedance. The op-amp has a "inverting" or (-) input and "noninverting" or (+) input and a single output. The op-amp is usually powered by a dual polarity power supply in the range of +/- 5 volts to +/- 15 volts. A simple dual polarity power supply is shown in the figure below which can be assembled with two 9 volt batteries.

Inverting Amplifier:

The op-amp is connected using two resistors RA and RB such that the input signal is applied in series with RA and the output is connected back to the inverting input through RB. The noninverting input is connected to the ground reference or the center tap of the dual polarity power supply. In operation, as the input signal moves positive, the output will move negative and visa versa. The amount of voltage change at the output relative to the input depends on the ratio of the two resistors RA and RB. As the input moves in one direction, the output will move in the opposite direction, so that the voltage at the inverting input remains constant or zero volts in this case. If RA is 1K and RB is 10K and the input is +1 volt then there will be 1 mA of current flowing through RA and the output will have to move to -10 volts to supply the same current through RB and keep the voltage at the inverting input at zero. The voltage gain in this case would be RB/RA or 10K/1K = 10. Note that since the voltage at the inverting input is always zero, the input signal will see a input impedance equal to RA, or 1K in this case. For higher input impedances, both resistor values can be increased.

Noninverting Amplifier:

The noninverting amplifier is connected so that the input signal goes directly to the noninverting input (+) and the input resistor RA is grounded. In this configuration, the input impedance as seen by the signal is much greater since the input will be following the applied signal and not held constant by the feedback current. As the signal moves in either direction, the output will follow in phase to maintain the inverting input at the same voltage as the input (+). The voltage gain is always more than 1 and can be worked out from Vgain = (1+ RB/RA).

Voltage Follower:

The voltage follower, also called a buffer, provides a high input impedance, a low output impedance, and unity gain. As the input voltage changes, the output and inverting input will change by an equal amount.

Operational Amplifiers Section Summary

The following is a summary of the different types of Operational Amplifiers and their configurations discussed in this tutorial section.

• The Operational Amplifier, or Op-amp as it is most commonly called, is an ideal amplifier with infinite Gain and Bandwidth when used in the Open-loop mode with typical d.c. gains of 100,000, or 100dB.
• The basic construction is of a 3-terminal device, 2-inputs and 1-output.
• An Operational Amplifier operates from a dual positive (+V) and an corresponding negative (-V) supply but they can also operate from a single DC supply voltage.
• It has Infinite Input impedance, (Z∞) resulting in "No current flowing into either of its two inputs" and zero input offset voltage "V1 = V2".
• It also has Zero Output impedance, (Z=0).
• Op-amps sense the difference between the voltage signals applied to the two input terminals and then multiply it by some pre-determined Gain, (A).
• This Gain, (A) is often referred to as the amplifiers "Open-loop Gain".
• Op-amps can be connected into two basic circuits, Inverting and Non-inverting.

The Two Basic Operational Amplifier Circuits

• The Open-loop gain called the Gain Bandwidth Product, or (GBP) can be very high and is a measure of how good an amplifier is.
• Very high GBP makes an Operational Amplifier circuit unstable as a microvolt input signal causes the output voltage to go into Saturation.
• By the use of suitable Feedback Resistor, (Rf) the overall gain of the amplifier can be accurately controlled.

Gain Bandwidth Product

• For Negative feedback, where the fed-back voltage is in "Anti-phase" to the input the overall gain of the amplifier is reduced.
• For Positive feedback, where the fed-back voltage is in "Phase" with the input the overall gain of the amplifier is increased.
• By connecting the output directly back to the negative input terminal, 100% feedback is achieved resulting in a Voltage Follower (buffer) circuit with a constant gain of 1 (Unity).
• Changing the fixed feedback resistor (Rf) for a Potentiometer, the circuit will have Adjustable Gain.
• The Differential Amplifier produces an output that is proportional to the difference between the 2 input voltages.

Differential and Summing Operational Amplifier Circuits

• Adding more input resistor to either the inverting or non-inverting inputs Voltage Adders or Summers can be made.
• Voltage follower op-amps can be added to the inputs of Differential amplifiers to produce high impedance Instrumentation amplifiers.
• The Integrator Amplifier produces an output that is the mathematical operation of integration.
• The Differentiator Amplifier produces an output that is the mathematical operation of differentiation.
• Both the Integrator and Differentiator Amplifiers have a Resistor and Capacitor connected across the op-amp and are affected by its RC time constant.
• In their basic form, Differentiator Amplifiers suffer from Instability and Noise but additional components can be added to reduce the overall Closed-loop gain.

Differentiator and Integrator Operational Amplifier Circuits

The Differentiator Amplifier

The basic Differentiator Amplifier circuit is a the exact opposite to that of the Integrator operational amplifier circuit that we saw in the previous tutorial. Here, the position of the capacitor and resistor have been reversed and now the Capacitor, C is connected to the input terminal of the inverting amplifier while the Resistor, Rf forms the negative feedback element across the operational amplifier. This circuit performs the mathematical operation of Differentiation, that is it produces a voltage output which is proportional to the input voltage's rate-of-change and the current flowing through the capacitor. In other words the faster or larger the change to the input voltage signal, the greater the input current, the greater will be the output voltage change in response becoming more of a "spike" in shape.

As with the integrator circuit, we have a resistor and capacitor forming an RC Network across the operational amplifier and the reactance (Xc) of the capacitor plays a major role in the performance of a Differentiator Amplifier.

Differentiator Amplifier Circuit

The capacitor blocks any DC content only allowing AC type signals to pass through and whose frequency is dependant on the rate of change of the input signal. At low frequencies the reactance of the capacitor is "High" resulting in a low gain (Rf/Xc) and low output voltage from the op-amp. At higher frequencies the reactance of the capacitor is much lower resulting in a higher gain and higher output voltage from the differentiator amplifier.

However, at high frequencies a differentiator circuit becomes unstable and will start to oscillate. This is due mainly to the First-order effect, which determines the frequency response of the op-amp circuit causing a Second-order response which, at high frequencies gives an output voltage far higher than what was expected. To avoid this the high frequency gain of the circuit needs to be reduced by adding an additional small value capacitor across the feedback resistor Rf.

Ok, some math's to explain what's going on. Since the node voltage of the operational amplifier at its inverting input terminal is zero, the current, i flowing through the capacitor will be given as:

The Charge on the Capacitor = Capacitance x Voltage across the Capacitor

The rate of change of this charge is

but dQ/dt is the capacitor current i

From which we have an ideal voltage output for the Differentiator Amplifier is given as:

Therefore, the output voltage Vout is a constant -Rf.C times the derivative of the input voltage Vin with respect to time. The minus sign indicates a 180⁰ phase shift because the input signal is connected to the inverting input terminal of the operational amplifier.

One final point to mention, the Differentiator Amplifier circuit in its basic form has two main disadvantages compared to the previous Integrator circuit. One is that it suffers from instability at high frequencies as mentioned above, and the other is that the capacitive input makes it very susceptible to random noise signals and any noise or harmonics present in the circuit will be amplified more than the input signal itself. This is because the output is proportional to the slope of the input voltage so some means of limiting the bandwidth in order to achieve closed-loop stability is required

Differentiator Waveforms

If we apply a constantly changing signal such as a Square-wave, Triangular or Sine-wave type signal to the input of a differentiator amplifier circuit the resultant output signal will be changed and whose final shape is dependant upon the RC time constant of the Resistor/Capacitor combination.

Improved Differentiator Amplifier

The basic single resistor and single capacitor differentiator circuit is not widely used to reform the mathematical function of Differentiation because of the two inherent faults mentioned above, Instability and Noise. So in order to reduce the overall closed-loop gain of the circuit at high frequencies, an extra Resistor, R2 is added to the input as shown below.

Improved Differentiator Amplifier Circuit

The circuit which we have now acts like a Differentiator amplifier at low frequencies and an amplifier with resistive feedback at high frequencies giving much better noise rejection. This then forms the basis of a Active High Pass Filter as seen before in the filters section.